Разбиение объектного пространства сцены путём построения octree-дерева
Have you ever stood and stared at it, Morpheus?
Marveled at its beauty. Its genius. Billions of people just living out their lives... oblivious.
Did you know that the first Matrix was designed to be a perfect human world?
Where none suffered, where everyone would be happy. It was a disaster. No one would accept the program.
Entire crops were lost.
Some believed we lacked the programming language to describe your perfect world.
But I believe that, as a species, human beings define their reality through suffering and misery.
Agent Smith. The Matrix.
Хотя в Королевстве статьи такого типа публикуются нечасто, я всё же попросил разрешения у Королевы сделать это, так как на тематику статей сайта никакие ограничения не накладываются, а сама программа написана на Object Pascal в среде Delphi. Для тех, кто читал мои ранние статьи по DirectX, хочу предупредить, что свои исследования в области прикладного API вроде DirectX и OpenGL я прекратил, и теперь больше занимаюсь алгоритмами, необходимыми для реализации трёхмерной графики. Ну да это так, к слову.
В компьютерной графике уже давно используются различные методы разделения объектного пространства на части с целью эффективной обработки только тех элементов сцены, которые наблюдатель может непосредственно увидеть через виртуальную "камеру". Всевозрастающая сложность геометрических сцен даёт прекрасную почву для исследования и разработки таких алгоритмов, причём если в компьютерной графике высокого уровня эти алгоритмы позволяют просто сократить время рендеринга сцены с месяцев до дней, то для графики реального времени они являются просто жизненно необходимыми - иначе понятие "интерактивная графика" просто бы отсутствовало.
Обычно тем, кто только начинает пробовать свои силы в 3D-пространстве, трудно понять, для чего же нужно разбиение пространства. Действительно, если опыты не выходят за рамки "солнышка и земли вокруг него", то заниматься этим нет смысла. Но допустим, мы взялись за рендеринг сложной сцены, вроде уровня Quake 3. Количество полигонов в сцене может достигать нескольких десятков тысяч (из года в год это значение неудержимо растёт), и если этот массив данных целиком отправлять на графический конвейер в каждом кадре, ни о какой интерактивности в игре и речи быть не может. Графический процессор будет тратить время на просчёт каждого полигона у каждого объекта, даже если в результате он жестоко не попадёт на экран.
В то же время лего заметить, что из всей сцены рельно в кадре постоянно видна лишь её небольшая часть. Очевидно, что объекты за "спиной" не будут видны однозначно, то же самое можно сказать об объектах, лежащих за границей зрения (рамками экрана). Если реализовать алгоритм, который позволяет выявить такие объекты, в результате его работы в графический ускоритель на обработку мы будем посылать сравнительно малую часть всей геометрии.
Здесь я собираюсь рассмотреть метод разделения объектного пространства, который называется octree (по-моему, от латинского octa - восемь, и английского tree - дерево). Восьмеричное дерево. Вообще подобные алгоритмы были разработаны ещё в 70-х годах, например, для точного описания ландшафта, но позже нашли своё применение в компьютерной графике.
Данный алгоритм производит разделение объектного пространства на восемь подпространств. Общую схему работы можно представить следующими шагами:
- Помещаем всю сцену в выровненный по осям куб. Этот куб описывает все элементы сцены и является корневым (root) узлом дерева.
- Проверяем количество примитивов в узле, и если полученное значение меньше определённого порогового, то производим связывание (ассоциацию) данных примитивов с узлом. Узел, с которым ассоциированы примитивы, является листом (leaf).
- Если же количество примитивов, попадающих в узел, больше порогового значения, производим разбиение данного узла на восемь подузлов (подпространств) путём деления куба двумя плоскостями. Мы распределяем примитивы, входящие в родительский узел, по дочерним узлам. Далее процесс идёт рекурсивно, т. е. для всех дочерних узлов, содержащих примитивы, выполняем пункт 2.
- Если количество примитивов в узле меньше или равно пороговому значению.
- Если рекурсия (количество делений) достигла какой-то определённой глубины вложенности.
- Если количество созданных узлов достигло порогового значения.
Самый простое и наглядное условие - это проверка на количество попадающих в узел геометрических примитивов (в нашем случае таким примитивом является треугольник). Это значение можно свободно варьировать, однако если вы хотите, чтобы скорость врендеринга была действительно хорошей, необходимо учитывать особенности современных видеокарт. Т. е. для отдельного вызова на графический конвейер необходимо подавать 200-300+ вершин, поэтому количество треугольников в узле должно быть достаточно большим - 100 и более. С другой стороны, бессмысленно делать это значение слишком большим - вне зависимости от того, видны ли все примитивы листа или нет, на графический конвейер они будут отправлены все, а это приведёт в большинстве случаев к бессмысленной обработке зачастую невидимой геометрии.
А теперь о том, как же именно применение данного алгоритма может помочь быстро откинуть части невидимой геометрии. Те элементы, что отображаются при рендеринге на экране, попадают в так называемый viewing frustum - пространство видимости. Графически оно выглядит вот так:
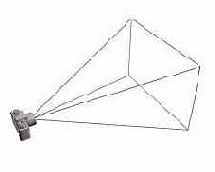
Рисунок 1. Viewing frustum
Теперь, в процессе рендеринга мы рекурсивно выполняем следующую процедуру: начиная с базового (root) куба, мы проверяем, попадает ли данный куб в поле зрения (viewing frustum). Если НЕТ - на этом всё и заканчивается, если же ДА - перемещаемся вглубь рекурсии на один шаг, т. е. поочерёдно проверяем видимость каждого из восьми подузлов корневого узла и т. д. Преимущество заключается в том, что если определено, что данный узел не виден, то можно смело не выводить и всю геометрию этого узла - она тоже будет не видна. Таким образом, ценой всего лишь нескольких проверок, мы отбросим значительную часть сцены. А в случае, если не виден корневой узел, на экран не будет выведено ничего. Сплошная экономия!
Представленная программа как раз и демонстрирует работу данного алгоритма. Из двоичного файла загружается сцена (я взял готовую модель для 3D Studio MAX), представляющая собой интерьер простой кухни. Для этой сцены строится octree-дерево, в качестве порогового количества примитивов в узле установлено значение 300. В сцене я специально разместил два высокополигональных объекта, чтобы можно было "прочувствовать" преимущество алгоритма. Это бутылки из-под кетчупа на столе. Как только они попадают в область видимости, fps резко падает, но при выходе их за пределы видимости fps возрастает. Если же направить камеру в пустоту, fps возрастает до максимально возможного, так как в этом случае рендеринг сцены не производится. Если бы мы не использовали алгоритм разбиения пространства, fps был бы неизменно низким, словно бутылки с кетчупом видны постоянно.
К сожалению, от достоинств алгоритма а нужно перейти к его недостаткам, коих немало. Первый из них - это возможное деления примитива ребрами кубов дерева, например, вот так:
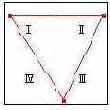
Рисунок 2. Проблемный случай
Обычно примитив относят к тому узлу, в пределах которого лежат вершины, образующие примитив. К какому из узлов отнести треугольник в данном случае? Казалось бы, взять да и отнести его к узлу I. Но так делать нельзя, и вот почему. Предположим, что мы связали треугольник с узлом I - тогда, если в процессе рендеринга мы определили, что узел I не виден, то и треугольник выведен не будет. Однако при этом возможна ситуация, когда узлы II и III будут в пространстве вида - полигон "выпадет" из сцены. Для избежания этого примитив относят к узлу, если хотя бы одна вершина примитива находится в пределах узла. В данном случае при таком подходе один и тот же треугольник будет ассоциирован с узлами I, II и III. В принципе, это не так уж страшно, так как данные можно индексировать, и этим избежать значительных расходов памяти. Однако в процессе рендеринга, если видны все три узла, полигон придётся вывести три раза. А это уже неприятно. Тем более, что такой полигон обычно не один, их множество.
Кое-где пишут, что это не так страшно, но я не согласен. Если такой примитив, например, покрыт большой текстурой, скорость вывода упадёт в несколько раз. Да и вообще, такие КрамольныЕ мысли в интерактивной графике недопустимы! Поэтому я поступил так: если примитив не полностью лежит в узле, его индекс заносится в отдельный массив. В процессе рендеринга ведётся учёт всех отрисованных "дробных" примитивов в специальном буфере, и если при выводе данного треугольника его индекс совпадёт с одним из индексов в буфере, мы не рисуем этот треугольник. Как показал опыт, помечать примитивы не так уж медленно, гораздо более медленно выводить геометрию три-четыре раза подряд.
Всё бы хорошо, да с делением примитива есть ещё одна проблема. Допустим, узлы I, II и III не видны. Однако узел IV может всё же попадать в поле зрения камеры, и видно, что частичка полигона всё же может выпасть, вот так:
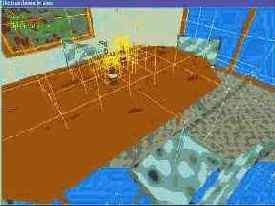
Рисунок 3. Полигон выпал
Что делать? Очевидно, что нельзя относить примитив к узлу, ориентируясь только на факт принадлежности вершины примитива к этому узлу. Наверное, все же вместо этого надо проверять, проходит ли РЕБРО примитива через пространство узла. Это может потребовать гораздо больше времени при построении дерева, но зато мы избежим выпадения полигонов. Кстати, структуру один раз построенного дерева можно записать в файл, и уже больше не строить его каждый раз при старте программы, а загружать из файла. В приведённом случае полигон придётся отнести ко всем четырём узлам.
Второй недостаток octree-дерева - это вывод всех объектов, находящихся в поле viewing frustum, но на самом деле в конечном счёте невидимых. Например, стена кухни может закрывать бутылки с кетчупом, но они всё равно будут отсылаться на конвейер (так как находятся в области viewing frustum), и fps будет низким. По-видимому, чистым octree-based алгоритмом здесь не обойтись, необходимо дополнительно реализовать так называемый Z-buffer, например, на тайловой основе. Коротко его работу можно описать так:
- Разбиваем проектную плоскость на некоторое число прямоугольников (тайлов), размером, например 32х32 пикселя.
- Если некий примитив полностью закрывает собой этот тайл, записываем в этот тайл среднее z-значение данного примитива
- При выводе очередного узла определяем, находятся ли его лицевые грани полностью в пределах тайла. Если это так и z-значение ближайшей вершины узла-куба больше z-значения тайла, то узел является скрытым, а значит, вся его геометрия тоже скрыта.
Вот примерно так можно будет определить, что бутылки с кетчупом находятся за стеной. К сожалению, всё это мною пока не реализовано :(
Представленная программа написана в IDE Delphi 5 без использования VCL, поэтому проблем с компиляцией в средах различных версий выше 3 я не предвижу. Используется API OpenGL (стандартный модудь Delphi opengl.pas), и дополнительный небольшой модуль myglext.pas, где я описал некоторые необходимые для работы программы расширения OpenGL (всё-таки удивительно, насколько стандартный модуль неполон в этом вопросе - ведь некоторые недокументированные в нём API-функции уже давно входят в ядро OpenGL и являются фундаментальными для 3D-графики). Для более эффективного рендеринга используется функция ядра glDrawElements() и не используются специфические расширения конкретных видеокарт, поэтому программа по идее должна работать на любом компьютере. Управление: мышью можно вращать камеру, а левой и правыми кнопками мыши двигать камеру вперёд-назад. Клавишей D включается/отключается отрисовка рёбер узлов дерева - можно как бы увидеть его структуру. Класиша W задаёт wireframe-режим.
Реализация алгоритма вполне работоспособна, но ещё недостаточно эффективна. Пораскинув мозгами, можно сделать несколько оптимизаций (чем автор и собирается заняться), а также попытаться избавиться от указанных мною ранее проблем.
Если вам есть что сказать — пишите
Скачать проект
